Hybridising standard reduced-order modelling methods with interpretable sparse neural networks for real-time patient-specific lung simulations

RICAM seminar

Alexandre Daby-Seesaram

alexandre.daby-seesaram@polytechnique.edu

LMS, École Polytechnique, Paris, France

Katerina Skardova

katerina.skardova@polytechnique.edu

LMS, École Polytechnique, Paris, France

Martin Genet

martin.genet@polytechnique.edu

LMS, École Polytechnique, Paris, France

October 22, 2024

Idiopathic Pulmonary Fibrosis

The role of mechanics

No identified bio-markers yet
A vicious circle has been hypothesised (F. Liu et al., 2010)
- Fibrotic tissues are stiffer
- Causing higher stresses
- Causing scarring
- Leading to the progress of the disease

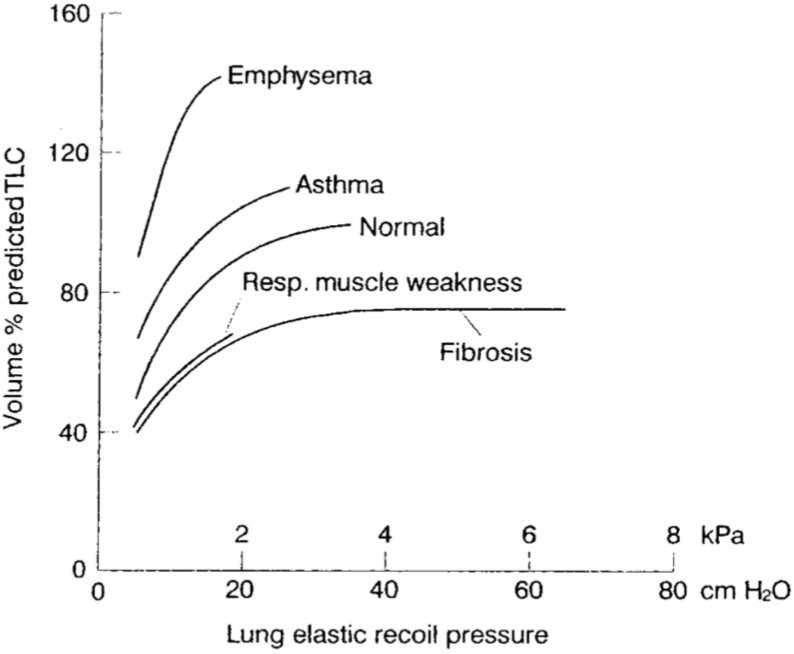
PV curves of healthy and diseased lungs, (Gibson, 2001)

Clinician’s perspective

Rely on mechanical analyses to better understand the disease and its progression

Idiopathic Pulmonary Fibrosis

Inspiration & expiration of diseased lungs

Digital twin from images

Objectives

Improved understanding of the physiological mechanisms
In silico prognostics
- Transfer tools to the clinic
- Patient-specific digital twins

Requirements

Mechanical model of the lung (Patte et al., 2022)

Uncertainty quantification (Peyraut & Genet, 2024)

Real-time estimation of the parameters

Lung poro-mechanics (Patte et al., 2022)

Weak formulation :

\[ \begin{cases} \int_{\Omega} \boldsymbol{\Sigma} : d_{\boldsymbol{u}}\boldsymbol{E}\left( \boldsymbol{u^*} \right) ~\mathrm{d}\Omega= W_{\text{ext}}\left(\boldsymbol{u},\boldsymbol{u^*}\right) ~\forall \boldsymbol{u^*} \in H^1_0\left(\Omega \right) \\[4mm] \int_{\Omega} \left(pf + \frac{\partial \Psi \left(\boldsymbol{u},\Phi_f\right)}{\partial \Phi_s}\right) \Phi_f^* ~\mathrm{d}\Omega= 0 ~\forall \Phi_f^* \end{cases} \label{eq:MechPb_lung} \]

Kinematics:

$\boldsymbol{F} = \boldsymbol{1} + \boldsymbol{\nabla}\boldsymbol{u}$ - deformation gradient
$\boldsymbol{C} = \boldsymbol{F}^T \cdot \boldsymbol{F}$ - right Cauchy-Green tensor
$\boldsymbol{E} = \frac{1}{2}\left(\boldsymbol{C} -\boldsymbol{1} \right)$ - Green-Lagrange tensor
- $I_1 = \text{tr}\left(\boldsymbol{C} \right)$ - first invariant of $\boldsymbol{C}$
- $I_2 = \frac{1}{2} \left(\text{tr}\left(\boldsymbol{C} \right)^2 - \text{tr}\left( \boldsymbol{C}^2f \right) \right)$

Behaviour

$\boldsymbol{\Sigma} = \frac{\partial \Psi_s + \Psi_f}{\partial \boldsymbol{E}} = \frac{\partial \Psi_s }{\partial \boldsymbol{E}} + p_f J \boldsymbol{C}^{-1}$ - The second Piola-Kirchhoff stress tensor
- $p_f = -\frac{\partial \Psi_s}{\partial \Phi_s}$ - fluid pressure
$\Psi_s\left(\boldsymbol{E}, \Phi_s \right) = W_{\text{skel}} + W_{\text{bulk}}$ \[\begin{cases} W_{\text{skel}} = \beta_1\left(I_1 - \text{tr}\left(I_d\right) -2 \text{ln}\left(\mathrm{det}\left(\boldsymbol{F} \right)\right)\right) + \beta_2 \left(I_2 -3 -4\text{ln}\left(\mathrm{det}\left(\boldsymbol{F} \right)\right)\right) + \alpha \left( e^{\delta\left(\mathrm{det}\left(\boldsymbol{F} \right)^2-1-2\text{ln}\left(\mathrm{det}\left(\boldsymbol{F} \right)\right) \right)} -1\right)\\ W_{\text{bulk}} = \kappa \left( \frac{\Phi_s}{1-\Phi_{f0}} -1 -\text{ln}\left( \frac{\Phi_s}{1-\Phi_{f0}}\right) \right) \end{cases}\]
$\Phi_s$ current volume fraction of solid pulled back on the reference configurations

Simpler mechanical problem - surrogate modelling

Parametrised (patient-specific) mechanical problem

\[ \boldsymbol{u} = \mathop{\mathrm{arg\,min}}_{H^1\left(\Omega \right)} \int_{\Omega} \Psi\left( \boldsymbol{E}\left(\boldsymbol{u}\left(\boldsymbol{x}, \left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}\right) \right) \right) ~\mathrm{d}\Omega- W_{\text{ext}}\left(\boldsymbol{x}, \left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}\right) \]

Kinematics:

$\boldsymbol{F} = \boldsymbol{1} + \boldsymbol{\nabla}\boldsymbol{u}$ - deformation gradient
$\boldsymbol{C} = \boldsymbol{F}^T \cdot \boldsymbol{F}$ - right Cauchy-Green tensor
$\boldsymbol{E} = \frac{1}{2}\left(\boldsymbol{C} -\boldsymbol{1} \right)$ - Green-Lagrange tensor
- $I_1 = \text{tr}\left(\boldsymbol{C} \right)$ - first invariant of $\boldsymbol{C}$

Behaviour - Saint Venant-Kirchhoff

$\Psi = \frac{\lambda}{2} \text{tr}\left(\boldsymbol{E}\right)^2 + \mu \boldsymbol{E}:\boldsymbol{E}$

Unstable under compression
$\nu = 0.48$ for quasi-incompressibility
- Soft tissues are often modelled as incompressible materials

Reduced-order model (ROM)

Build a surrogate model
- Parametrised solution
No computations online
On the fly evaluation of the model
- Real-time parameters estimation

II - Methods

\[ \definecolor{BleuLMS}{RGB}{1, 66, 106} \definecolor{VioletLMS}{RGB}{77, 22, 84} \definecolor{TealLMS}{RGB}{0, 103, 127} % \definecolor{BleuLMS2}{RGB}{0, 103, 202} \definecolor{BleuLMS2}{RGB}{0, 169, 206} \definecolor{BleuLMPS}{RGB}{105, 144, 255} \definecolor{accentcolor}{RGB}{1, 66, 106} \definecolor{GreenLMS}{RGB}{0,103,127} \definecolor{LGreenLMS}{RGB}{67,176,42} \definecolor{RougeLMS}{RGB}{206,0,55} \]

Mechanical solution interpolation

Reduced-order modelling

Hybrid Neural Network Proper Generalised Decomposition

Interpolation of the solution

FEM finite admissible space

\[ \mathcal{U}_h = \left\{\boldsymbol{u}_h \; | \; \boldsymbol{u}_h \in \text{Span}\left( \left\{ N_i^{\Omega}\left(\boldsymbol{x} \right)\right\}_{i \in \mathopen{~[\!\![~}1,N\mathclose{~]\!\!]}} \right)^d \text{, } \boldsymbol{u}_h = \boldsymbol{u}_d \text{ on }\partial \Omega_d \right\} \]

Interpretabilty
Kronecker propriety
- Easy to prescribe Dirichlet boundary conditions

Mesh adaptation not directly embedded in the method

Physics Informed Neural Networks (PINNs)

\[ \boldsymbol{u} \left(x_{0,0,0} \right) = \sum\limits_{i = 0}^C \sum\limits_{j = 0}^{N_i} \sigma \left( \sum\limits_{k = 0}^{M_{i,j}} b_{i,j}+\omega_{i,j,k}~ x_{i,j,k} \right) \]

All interpolation parameters are trainable
Benefits from ML developments

Not easily interpretable
Difficult to prescribe Dirichlet boundary conditions

HiDeNN framework (Y. Liu et al., 2023; Park et al., 2023; Zhang et al., 2021)
- Best of both worlds
- Reproducing FEM interpolation with constrained sparse neural networks
- $N_i^{\Omega}$ are SNN with constrained weights and biases
- Fully interpretable parameters
- Continuous interpolated field that can be automatically differentiated
- Runs on GPUs

Illustration of Finite Element Neural Network Interpolation (FENNI)

Solving the mechanical problem

Solving the mechanical problems amounts to finding the continuous displacement field minimising the potential energy \[E_p\left(\boldsymbol{u}\right) = \frac{1}{2} \int_{\Omega}\boldsymbol{E} : \mathbb{C} : \boldsymbol{E} ~\mathrm{d}\Omega- \int_{\partial \Omega_N}\boldsymbol{F}\cdot \boldsymbol{u} ~\mathrm{d}A- \int_{\Omega}\boldsymbol{f}\cdot\boldsymbol{u}~\mathrm{d}\Omega. \]

In practice

Compute the loss $\mathcal{L} := E_p$
Find the parameters minimising the loss
- Rely on state-of-the-art optimizers (ADAM, LBFGS, etc.)

Degrees of freedom (Dofs)

Nodal values (standard FEM Dofs)
Nodal coordinates (Mesh adaptation)
- hr-adaptivity

r-adaptivity

rh-adaptivity

h-adaptivity: red-green refinement

technical details:

Dofs (initially)	$569~438$
Training time (s)	$7$
GPU (V100)	1
CPUs	40

Results

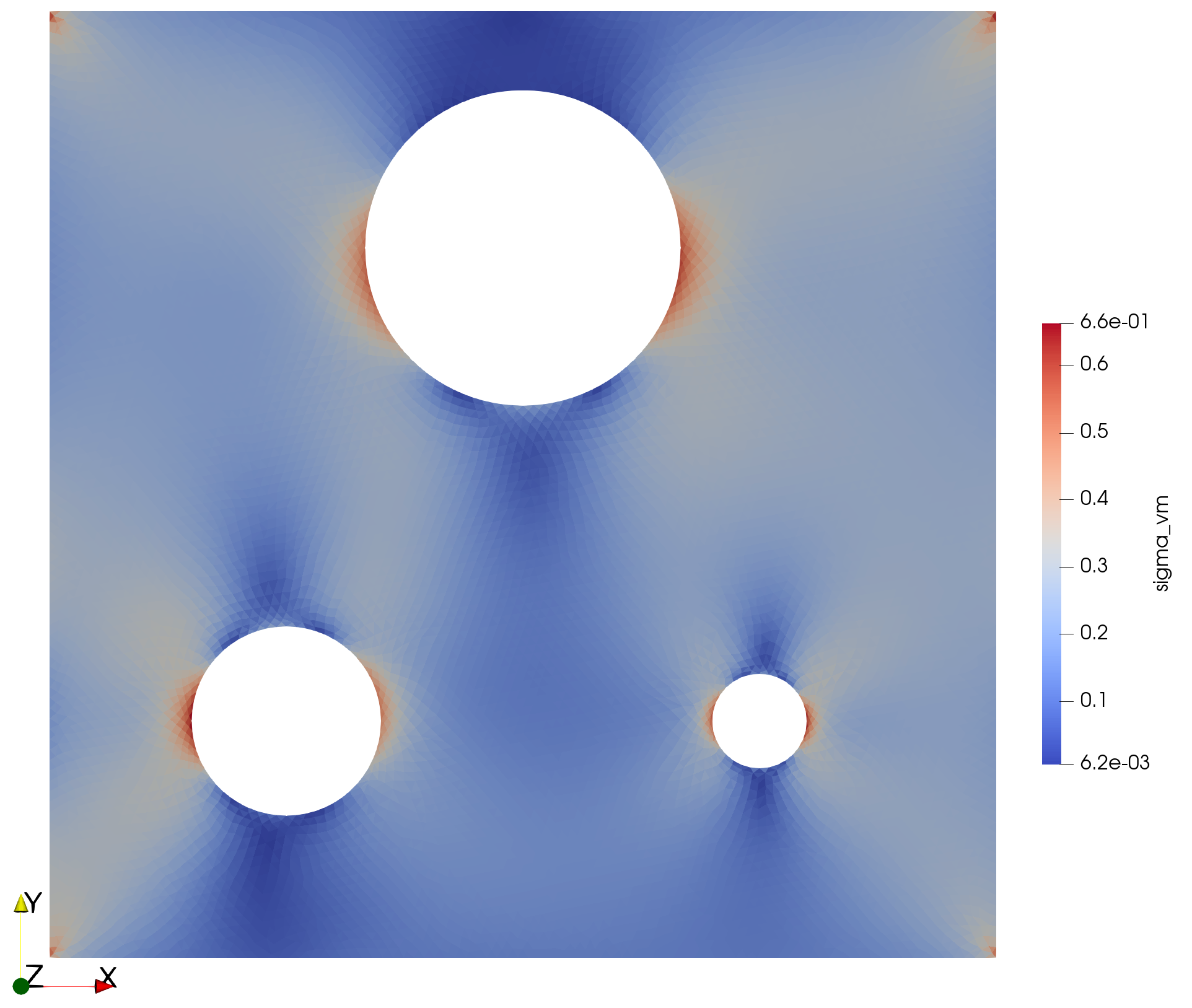
HR-adaptivity benefits

Improved maximum stress accuracy
Improved overall solution as well at lower cost

Surrogate model

Still just a snapshot
Need to take into account the parametrisation

Reduced-order modelling (ROM)

Low-rank approximation of the solution to avoid the curse of dimensionality with $\beta$ parameters

Full-order discretised model

$N$ spatial shape functions
- Span a finite spatial space of dimension $N$
Requires computing $N\times \beta$ associated parametric functions

Reduced-order model

$m \ll N$ spatial modes
- Similar to global shape functions
- Span a smaller space
Galerkin projection

Finding the reduced-order basis

Linear Normal Modes (eigenmodes of the structure) (Hansteen & Bell, 1979)
- Do not account for the loading and behaviour specifics
Proper Orthogonal Decomposition (Chatterjee, 2000; Radermacher & Reese, 2013)
- Require wise selection of the snapshots and costly computations
Reduced basis method (Maday & Rønquist, 2002) with EIM (Barrault et al., 2004)
- Rely on prior expensive computations

Proper Generalised Decomposition (PGD)

PGD: (Chinesta et al., 2011; Ladevèze, 1985)

Tensor decomposition

Separation of variables
Low-rank $m$
$\textcolor{BleuLMPS}{\overline{\boldsymbol{u}}_i(\boldsymbol{x})}$ Space modes
$\textcolor{LGreenLMS}{\lambda_i^j(\mu^j)}$ Parameter modes

\[\textcolor{VioletLMS}{\boldsymbol{u}}\left(\textcolor{BleuLMPS}{\boldsymbol{x}}, \textcolor{LGreenLMS}{\mu}\right) = \sum\limits_{i=0}^{m}\textcolor{BleuLMPS}{\overline{u}_i\left(x\right)}\textcolor{LGreenLMS}{\lambda_i\left(\mu\right)}\]

Discretised problem

From $N\times N_{\mu}$ unknowns to $m\times\left(N + N_{\mu}\right)$

Historicaly space-time PGD: $\textcolor{VioletLMS}{\boldsymbol{u}}\left(\textcolor{BleuLMPS}{\boldsymbol{x}}, \textcolor{LGreenLMS}{t}\right) = \sum\limits_{i=0}^{m}\textcolor{BleuLMPS}{\overline{u}_i\left(x\right)}\textcolor{LGreenLMS}{\lambda_i\left(t\right)}$

Elasto-(visco)plastic problems (Boisse et al., 1990)
Single extra-coordinate
Extra-parametrisation accounted for in multi-query framework
- Relying on non-incremental solver (LATIN) (Néron et al., 2015)

Proper Generalised Decomposition (PGD)

PGD: (Chinesta et al., 2011; Ladevèze, 1985)

Tensor decomposition - extra-coordinates

Separation of variables
Low-rank $m$
$\textcolor{BleuLMPS}{\overline{\boldsymbol{u}}_i(\boldsymbol{x})}$ Space modes
$\textcolor{LGreenLMS}{\lambda_i^j(\mu^j)}$ Parameter modes

\[ \textcolor{VioletLMS}{\boldsymbol{u}}\left(\textcolor{BleuLMPS}{\boldsymbol{x}}, \textcolor{LGreenLMS}{\left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}}\right) = \sum\limits_{i=1}^m \textcolor{BleuLMPS}{\overline{\boldsymbol{u}}_i(\boldsymbol{x})} ~\textcolor{LGreenLMS}{\prod_{j=1}^{\beta}\lambda_i^j(\mu^j)} \]

Discretised problem

From $N\times\prod\limits_{j=1}^{~\beta} N_{\mu}^j$ unknowns to $m\times\left(N + \sum\limits_{j=1}^{\beta} N_{\mu}^j\right)$

Finding the tensor decomposition by minimising the energy \[ \left(\left\{\overline{\boldsymbol{u}}_i \right\}_{i\in \mathopen{~[\!\![~}1,m\mathclose{~]\!\!]}},\left\{\lambda_i^j \right\}_{ \begin{cases} i\in \mathopen{~[\!\![~}1,m\mathclose{~]\!\!]}\\ j\in \mathopen{~[\!\![~}1,\beta \mathclose{~]\!\!]} \end{cases} } \right) = \mathop{\mathrm{arg\,min}}_{ \begin{cases} \left(\overline{\boldsymbol{u}}_1, \left\{\overline{\boldsymbol{u}}_i \right\} \right) & \in \mathcal{U}\times \mathcal{U}_0 \\ \left\{\left\{\lambda_i^j \right\}\right\} & \in \left( \bigtimes_{j=1}^{~\beta} \mathcal{L}_2\left(\mathcal{B}_j\right) \right)^{m-1} \end{cases}} ~\underbrace{\int_{\mathcal{B}}\left[E_p\left(\boldsymbol{u}\left(\boldsymbol{x},\left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}\right), \mathbb{C}, \boldsymbol{F}, \boldsymbol{f} \right) \right]\mathrm{d}\beta}_{\mathcal{L}} \label{eq:min_problem} \]

Proper Generalised Decomposition (PGD)

Building the low-rank tensor decomposition greedily (Ladevèze, 1985; Nouy, 2010)

\[ \boldsymbol{u}\left(\boldsymbol{x}, \left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}\right) = \overline{\boldsymbol{u}}(\boldsymbol{x}) ~\prod_{j=1}^{\beta}\lambda^j(\mu^j) \]

\[ \boldsymbol{u}\left(\boldsymbol{x}, \left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}\right) = \textcolor{RougeLMS}{\sum\limits_{i=1}^{2}} \overline{\boldsymbol{u}}_{\textcolor{RougeLMS}{i}}(\boldsymbol{x}) ~\prod_{j=1}^{\beta}\lambda_{\textcolor{RougeLMS}{i}}^j(\mu^j) \]

\[ \boldsymbol{u}\left(\boldsymbol{x}, \left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}\right) = \sum\limits_{i=1}^{\textcolor{RougeLMS}{m}} \overline{\boldsymbol{u}}_i(\boldsymbol{x}) ~\prod_{j=1}^{\beta}\lambda_i^j(\mu^j) \]

Greedy algorithm

Start with a single mode
Minimise the loss until stagnation

Add a new mode
If loss decreases, continue training

Else stop and return the converged model

The PGD is

An a priori ROM techniques
- Building the model from scratch on the fly
No full-order computations
Reduced-order basis tailored to the specifics of the problem (Daby-Seesaram et al., 2023)

Note

Training of the full tensor decomposition, not only the $m$-th mode
Actual minimisation implementation of the PGD
No need to solve a new problem for any new parameter
- The online stage is a simple evaluation of the tensor decomposition

Neural Network PGD

Graphical implementation of Neural Network PGD

\[ \boldsymbol{u}\left(\textcolor{BleuLMPS}{\boldsymbol{x}}, \textcolor{LGreenLMS}{\left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}}\right) = \sum\limits_{i=1}^m \textcolor{BleuLMPS}{\overline{\boldsymbol{u}}_i(\boldsymbol{x})} ~\textcolor{LGreenLMS}{\prod_{j=1}^{\beta}\lambda_i^j(\mu^j)} \]

Interpretable NN-PGD

No black box
- Fully interpretable implementation
- Great transfer learning capabilities
Straightforward implementation
- Benefiting from current ML developments

Straightforward definition of the physical loss using auto-differentiation

def Loss(model,x,detJ,mu):
  
    u = model.space_mode(x)
    eps = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u))
    lmbda = model.parameter_mode(mu)
    W_int = torch.einsum('ij,ejm,eil,em,mp...,lp...,p->',C,eps,eps,detJ,lmbda,lmbda, mu)

    return 0.5*W_int/mu.shape[0]

Summary of the framework

FENNI-PGD

III - Preliminary results

Surrogate model in use

Training and convergence proprieties

Hybridising ROM with FENNI

Open-source code

pip install NeuROM-Py

All the figures of the papers are in Jupyter’s books
- Greater reproductibility

Stiffness and external forces parametrisation

Illustration of the surrogate model in use

Parameters

Parametrised stiffness $E$
Parametrised external force $\boldsymbol{f} = \begin{bmatrix} ~ \rho g \sin\left( \theta \right) \\ -\rho g \cos\left( \theta \right) \end{bmatrix}$

NeuROM

NN-PGD

Immediate evaluation of the surrogate model
Straightforward differentiation capabilities regarding the input parameters

Convergence of the greedy algorithm

Construction of the ROB

New modes are added when the loss’s decay cancels out
Adding a new mode gives extra latitude to improve predictivity

Accuracy with regards to FEM solutions

Solution	Error
$Configuration 1: ( E = 3.8 ^{-3} ) MPa, ( = 241^)$	$Configuration 1 Error: ( E = 3.8 ^{-3} ) MPa, ( = 241^)$
$Configuration 2: ( E = 3.1 ^{-3} ) MPa, ( = 0^)$	$Configuration 2 Error: ( E = 3.1 ^{-3} ) MPa, ( = 0^)$

$E$ (kPa)	$\theta$ (rad)	Relative error
3.80	1.57	$1.12 \times 10^{-3}$
3.80	4.21	$8.72 \times 10^{-4}$
3.14	0	$1.50 \times 10^{-3}$
4.09	3.70	$8.61 \times 10^{-3}$
4.09	3.13	$9.32 \times 10^{-3}$
4.62	0.82	$2.72 \times 10^{-3}$
5.01	2.26	$5.35 \times 10^{-3}$
6.75	5.45	$1.23 \times 10^{-3}$

Multi-level training

Strategy

The interpretability of the NN allows
- Great transfer learning capabilities
  - Start with coarse (cheap) training
  - Followed by fine tuning, refining all modes
Extends the idea put forward by (Giacoma et al., 2015)

Note

The structure of the Tensor decomposition is kept throughout the multi-level training
Last mode of each level is irrelevant by construction
- It is removed before passing onto the next refinement level

Heterogeneous stiffness

Bi-stiffness structure with unknown
- Stiffness jump $\Delta E$
- Jump position $\alpha$

Towards the parametrisation of the disease’s progression
- Can be adapted to different stages of the diseases
- Different physiological initial stiffness

Heterogeneous stiffness

Convergence process

Larger Kolmogorov n-with’s example
Similar behaviour in constructing the reduced-order basis
- Adding a mode leads to a recovery in loss decay
- This recovery decreases until global stagnation

Curse of dimensionality in computing the loss

Computing the non-linear loss using einsum relies on the tensor decomposition and broadcasting to remain efficient
Although the displacement is represented through a tensor decomposition $\boldsymbol{u}\left(\boldsymbol{x}, \left\{\mu_i\right\}_{i \in \mathopen{~[\!\![~}1, \beta \mathclose{~]\!\!]}}\right) = \boldsymbol{\overline{u}}_i \prod_{j=1}^{\beta}\lambda_i^j(\mu^j)$, some non-linear mapping of that function cannot be easily computed on the independent modes but requires building the full-order solution tensor which leads to prohibitive training costs.

More physically sound behaviour laws

Incompressible Neo-Hookean elastic behaviour: Improve the elastic behaviour \[ \begin{cases} \Psi = C_1(\text{tr}\left(\boldsymbol{C}-\boldsymbol{1}\right)) + f\left(\text{ln}\left(\text{det}\left( \boldsymbol{F}\right) \right) \right)\\[2mm] \left(\text{det}\boldsymbol{F} - 1\right)^2 = 0 \end{cases} \]

Sparse sampling of the hypercube

One idea might be to look at sparse sampling of the parameters sets over which the loss function is computed, using a (greedy) LHS in the parametric space for instance instead of computing the integral of the potential energy over the full parametric hypercube
- Similar idea than in (Lu et al., 2018) but applied on PDEs and not data compression
The underlying idea being that the solution interpolation being constrained to be low-rank by the TD, such sparse training might suffice

Conclusion

Robust and straightforward general implementation of a NN-PGD
- Interpretable
- Benefits from all recent developments in machine learning
Surrogate modelling of parametrised PDE solution
- Promising results on simple toy case

Perspectives for patient-specific applications

Implementation of the poro-mechanics lung model (Patte et al., 2022)
Parametrisation of the segmented geometries
- Variational encoder to reduce the segmentation’s parametrisation’s dimensionnality
Application to real-time lung parameters estimation
Error quantification on the estimated parameters

Technical perspectives

3D implementation
Geometry based h refinement
Do not hesitate to check the Github page


Github page

References

Barrault, M., Maday, Y., Nguyen, N. C., & Patera, A. T. (2004). An “empirical interpolation” method: Application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathematique, 339(9), 667–672. https://doi.org/10.1016/j.crma.2004.08.006

Boisse, Ph., Bussy, P., & Ladeveze, P. (1990). A new approach in non-linear mechanics: The large time increment method. International Journal for Numerical Methods in Engineering, 29(3), 647–663. https://doi.org/10.1002/nme.1620290312

Chatterjee, A. (2000). An introduction to the proper orthogonal decomposition. Current Science, 78(7), 808–817. https://www.jstor.org/stable/24103957

Chinesta, F., Ladeveze, P., & Cueto, E. (2011). A Short Review on Model Order Reduction Based on Proper Generalized Decomposition. Archives of Computational Methods in Engineering, 18(4), 395–404. https://doi.org/10.1007/s11831-011-9064-7

Daby-Seesaram, A., Fau, A., Charbonnel, P.-É., & Néron, D. (2023). A hybrid frequency-temporal reduced-order method for nonlinear dynamics. Nonlinear Dynamics, 111(15), 13669–13689. https://doi.org/10.1007/s11071-023-08513-8

Giacoma, A., Dureisseix, D., Gravouil, A., & Rochette, M. (2015). Toward an optimal a priori reduced basis strategy for frictional contact problems with LATIN solver. Computer Methods in Applied Mechanics and Engineering, 283, 1357–1381. https://doi.org/10.1016/j.cma.2014.09.005

Gibson, G. J. (2001). Lung volumes and elasticity. Clinics in Chest Medicine, 22(4), 623–635, vii. https://doi.org/10.1016/s0272-5231(05)70056-3

Hansteen, O. E., & Bell, K. (1979). On the accuracy of mode superposition analysis in structural dynamics. Earthquake Engineering & Structural Dynamics, 7(5), 405–411. https://doi.org/10.1002/eqe.4290070502

Ladevèze, P. (1985). Sur une famille d’algorithmes en mécanique des structures. Comptes-Rendus Des Séances de l’Académie Des Sciences. Série 2, Mécanique, Physique, Chimie, Sciences de l’univers, Sciences de La Terre, 300(2).

Liu, F., Mih, J. D., Shea, B. S., Kho, A. T., Sharif, A. S., Tager, A. M., & Tschumperlin, D. J. (2010). Feedback amplification of fibrosis through matrix stiffening and COX-2 suppression. Journal of Cell Biology, 190(4), 693–706. https://doi.org/10.1083/jcb.201004082

Liu, Y., Park, C., Lu, Y., Mojumder, S., Liu, W. K., & Qian, D. (2023). HiDeNN-FEM: A seamless machine learning approach to nonlinear finite element analysis. Computational Mechanics, 72(1), 173–194. https://doi.org/10.1007/s00466-023-02293-z

Lu, Y., Blal, N., & Gravouil, A. (2018). Adaptive sparse grid based HOPGD: Toward a nonintrusive strategy for constructing space-time welding computational vademecum. International Journal for Numerical Methods in Engineering, 114(13), 1438–1461. https://doi.org/10.1002/nme.5793

Maday, Y., & Rønquist, E. M. (2002). A Reduced-Basis Element Method. Journal of Scientific Computing, 17(1), 447–459. https://doi.org/10.1023/A:1015197908587

Néron, D., Boucard, P.-A., & Relun, N. (2015). Time-space PGD for the rapid solution of 3D nonlinear parametrized problems in the many-query context: PGD FOR THE RAPID SOLUTION OF NONLINEAR PARAMETRIZED PROBLEMS. International Journal for Numerical Methods in Engineering, 103(4), 275–292. https://doi.org/10.1002/nme.4893

Nouy, A. (2010). A priori model reduction through Proper Generalized Decomposition for solving time-dependent partial differential equations. Computer Methods in Applied Mechanics and Engineering, 199(23-24), 1603–1626. https://doi.org/10.1016/j.cma.2010.01.009

Park, C., Lu, Y., Saha, S., Xue, T., Guo, J., Mojumder, S., Apley, D. W., Wagner, G. J., & Liu, W. K. (2023). Convolution hierarchical deep-learning neural network (C-HiDeNN) with graphics processing unit (GPU) acceleration. Computational Mechanics, 72(2), 383–409. https://doi.org/10.1007/s00466-023-02329-4

Patte, C., Genet, M., & Chapelle, D. (2022). A quasi-static poromechanical model of the lungs. Biomechanics and Modeling in Mechanobiology, 21(2), 527–551. https://doi.org/10.1007/s10237-021-01547-0

Peyraut, A., & Genet, M. (2024, May). Quantification d’incertitudes pour la modélisation pulmonaire personnalisée. 16ème Colloque National En Calcul de Structures. https://hal.science/hal-04611023

Radermacher, A., & Reese, S. (2013). A comparison of projection-based model reduction concepts in the context of nonlinear biomechanics. Archive of Applied Mechanics, 83(8), 1193–1213. https://doi.org/10.1007/s00419-013-0742-9

Zhang, L., Cheng, L., Li, H., Gao, J., Yu, C., Domel, R., Yang, Y., Tang, S., & Liu, W. K. (2021). Hierarchical deep-learning neural networks: Finite elements and beyond. Computational Mechanics, 67(1), 207–230. https://doi.org/10.1007/s00466-020-01928-9

Appendix - Orthonormalisation of the ROB

To ensure orthonormality of the RON, a Gramm-Schmidt like algorithm can be performed

\[ \boldsymbol{u}_{m+1} = \sum_{i=1}^{m} \underbrace{(\lambda_i + \lambda_{m+1} ~ \overline{\boldsymbol{u}}_i^T \overline{\boldsymbol{u}})}_{\mathring{\lambda}_i} \overline{\boldsymbol{u}}_i + \lambda_{m+1} \underbrace{\left(\overline{\boldsymbol{u}}_{m+1} - \sum_{i=1}^{m} ( \overline{\boldsymbol{u}}_i^T \overline{\boldsymbol{u}}) \overline{\boldsymbol{u}}_i\right)}_{\mathring{\overline{\boldsymbol{u}}}_{m+1}} \]

\[\overline{\boldsymbol{u}}_{m+1} \longleftarrow \frac{\mathring{\overline{\boldsymbol{u}}}_{m+1}}{\Vert\mathring{\overline{\boldsymbol{u}}}_{m+1} \Vert_{\mathbb{K}}} \]

\[ \lambda_{m+1} \longleftarrow \lambda_{m+1} \Vert\mathring{\overline{\boldsymbol{u}}}_{m+1} \Vert_{\mathbb{K}} \] \[ \{\lambda_i\}_{i\in\mathopen{~[\!\![~}1,m\mathclose{~]\!\!]}} \gets \{\mathring{\lambda}_i\}_{i\in\mathopen{~[\!\![~}1,m\mathclose{~]\!\!]}} \]

Much more tricky with more thant 2 parameters in the tensor decomposition

Appendix - PGD of a known field & eigen value problem

Let $\boldsymbol{u}\left(\boldsymbol{x},t\right)$ defined on $t \in I = \left[0,T\right]$ and $\boldsymbol{x} \in \Omega \subset \mathbb{R}^d$. Let’s look at the single mode decomposition: \[\left(\boldsymbol{\overline{u}}_1, \lambda_1\right) = \mathop{\mathrm{arg\,min}}_{\mathcal{U},\mathcal{I}} \left\Vert \boldsymbol{u} - \boldsymbol{\overline{u}}_1 \lambda_1 \right\Vert^2\]

\[\Leftrightarrow\int_{I\times\Omega}\left(\boldsymbol{u} - \boldsymbol{\overline{u}}_1 \lambda_1 \right)\left( \boldsymbol{\overline{u}}^* \lambda^* \right) ~\mathrm{d}\Omega\mathrm{d}t = 0 \forall \lambda^* \in \mathcal{I}, \forall \boldsymbol{\overline{u}}^* \in \mathcal{U}\]

\[\Leftrightarrow\begin{cases} \lambda_1\left(t \right) = \frac{\int_{\Omega}\boldsymbol{u}\left(\boldsymbol{x},t \right)\boldsymbol{\overline{u}}_1 ~\mathrm{d}\Omega}{\int_{\Omega} \boldsymbol{\overline{u}}_1^2 ~\mathrm{d}\Omega} = f\left( \lambda_1 \right) \\ \boldsymbol{\overline{u}}_1\left(\boldsymbol{x} \right) =\frac{\int_{I}\boldsymbol{u}\left(\boldsymbol{x},t \right) \lambda_1 \mathrm{d}t}{\int_{I} \lambda_1^2 \mathrm{d}t} = g\left( \boldsymbol{\overline{u}}_1 \right) \end{cases}\]

\[ \Leftrightarrow \lambda_1 = f \circ g \left( \lambda_1 \right)\]

\[ \Leftrightarrow \underbrace{\int_{\Omega} \boldsymbol{u}\int_{I}\boldsymbol{u}\lambda_1 \mathrm{d}t ~\mathrm{d}\Omega}_{T\left(\lambda_1 \right)} = \underbrace{\frac{\int_{\Omega \left(\int_I \boldsymbol{u}\lambda_1\mathrm{d}t \right)^2 ~\mathrm{d}\Omega}}{\int_I \lambda_1^2\mathrm{d}t}}_ {\omega^2}\lambda_1\]

$\left\Vert \boldsymbol{u} - \boldsymbol{\overline{u}}_1\lambda_1\right\Vert = \left\Vert \boldsymbol{u}\right\Vert^2 - R\left( \lambda_1 \right)$

with

$R\left( \lambda_1 \right) = \omega^2$

Eigen value problem

Equivalent to searching for the stationarity of a rayleigh’s quotient
It can be shown that minimising the truncation error amounts to fining the largest eigenvalues

In practice

Modes are computed greedily
- Less optimal
The temporal modes can be updated
- improved accuracy

Appendix - Einstein notation

Writing the linear elasticity with the einstein notation:

\[ W_{\text{int}} = \int_{\mathcal{B}}\frac{1}{2} \int_{\Omega}\mathcal{\boldsymbol{\varepsilon}}: \mathbb{C} : \mathcal{\boldsymbol{\varepsilon}}~\mathrm{d}\Omega\mathrm{d}\beta = \frac{1}{2} K_{ij} \mathcal{\boldsymbol{\varepsilon}}_{j}\left(\boldsymbol{\overline{u}}_{em}\right) \mathcal{\boldsymbol{\varepsilon}}_{i}\left(\boldsymbol{\overline{u}}_{el}\right) \mathrm{det}\left(J\right)_{em} \lambda^{\left(1\right)}_{mp} \lambda^{\left(2\right)}_{lp} \lambda^{\left(1\right)}_{mt} \lambda^{\left(2\right)}_{lt} E_p\]

\(E\) (kPa)	\(\theta\) (rad)	Relative error
3.80	1.57	\(1.12 \times 10^{-3}\)
3.80	4.21	\(8.72 \times 10^{-4}\)
3.14	0	\(1.50 \times 10^{-3}\)
4.09	3.70	\(8.61 \times 10^{-3}\)
4.09	3.13	\(9.32 \times 10^{-3}\)
4.62	0.82	\(2.72 \times 10^{-3}\)
5.01	2.26	\(5.35 \times 10^{-3}\)
6.75	5.45	\(1.23 \times 10^{-3}\)